All about Mathematics^^: Oktober 2018

Holaaaaa, bertemu lagi dengan saya wkwk jangan bosen yaaa:p di blog kali ini saya akan memberikan penjelasan tentang Turunan Fungsi . Yuk langsung ajaaaa....

A. Definisi Turunan Fungsi

=> Turunan fungsi adalah fungsi lain dari suatu fungsi sebelumnya, misalnya fungsi f menjadi f' yang mempunyai nilai tidak beraturan.

B. Perbedaan Differensial dan Derivative

Diferensial (Perubahan)

Turunan adalah hasil pembagian antara 2 buah diferensial.Sebagai contoh,Jika kita mengatakan bahwa "turunan dari adalah ", maka pernyataan itu adalah BENAR, karena . Tapi, akan SALAH jika turunan disamakan dengan diferensial. Jika kita mengatakan bahwa "diferensial dari adalah ", maka pernyataan itu adalah SALAH. Kalau ingin betulnya, harus seperti ini: "diferensial dari adalah dikalikan dengan diferensial x" atau dapat ditulis begini:
Lalu, kenapa dinamakan diferensial?Ingat-ingat kembali rumus turunan:
Diferensial adalah selisih variabel (Ingat "difference" dalam bahasa inggris artinya "beda", bukan?).. Sekadar mengingatkan, di rumus di atas, maka x adalah variabel bebas sedangkan y adalah variabel terikat.. Sebenarnya, bisa saja rumusnya begini:
Di atas maka y adalah variabel bebas sedangkan nilai x terikat terhadap variabel y.Jika , maka

Derivative ( Turunan)

         Proses penurunan sebuah fungsi disebut proses pendiferensian atau diferensiasi,merupakan penentuan limit suatu kuosien diferensiasi dalam pertambahan variable bebas yang sangat kecil atau mendekati nol.
Hasil dari proses pendiferensiasi disebut turunan atau derivative.
Dengan demikian : Jika y = f (x)
Maka kuosien diferensinya : ( kd) :
Dan turunan fungsinya :
Contoh
Persamaan                  y = 4x²– x
Kuosien difrensiasi :   = 8 x + 3 x -1
                                      = 8x +3(0) -1
                                      = 8x – 1
Jadi turunan (derivatif) dari fungsi y = 4 x² – x adalah: 8 x – 1

C. Kaidah-Kaidah Operasional Turunan

D. Rumus Umum Turunan

Jika kalian memepertanyakan darimana kita mendapatkan rumus dasar di atas? Well, keingintahuan yang mengagumkan, kawan. Tetaplah berpikir kritis seperti itu. dan insyaallah akan saya share di postingan saya yang selanjutnya.

Ok, kembali ke pembuktian rumus umum turunan suatu polinom f(x)=xⁿ. Jika f(x) pada rumus dasar turunan di atas kita ganti dengan xⁿ, maka:

Kemudian kira gunakan rumus Binomial Newton untuk menjabarkan (x+ Dx)ⁿ di atas. Dimana kita telah mengetahui bahwa rumus Binomial Newton sebagai berikut:

Dari rumus ini, maka kita dapatkan a=x dan b =Dx, sehingga:

Maka, persamaan (1) di atas menjadi:

Jadi, jika f(x)=xⁿ, maka turunan pertama dari fungsi tersebut adalah f’(x)=n.x^n-1.

E. Turunan Penjumlahan, Selisih, Perkalian, dan Pembagian

Turunan Fungsi Penjumlahan dan Selisih

Bila y = f(x) = u(x) + v(x) di mana turunan dari u(x) adalah u'(x) dan turunan dari v(x) adalah v'(x), maka turunan dari f(x) adalah f ′(x) = u'(x) + v'(x). Begitu juga bila f(x) = u(x) – v(x), maka f ′(x) = u'(x) + v'(x). Jadi, jika y = u ±v, maka y' = u' ± v'.

Nah itu teorinya, agar lebih jelasnya, coba anda pelajarilah beberapa contoh soal berikut ini

Contoh Soal 1

Carilah f ′(x) jika f(x) = 3x² + 7x

Penyelesaian:

f(x) = 3x² + 7x

Misal:

u = 3x² → u' = 3⋅2⋅x² ^{– 1} = 6x¹ = 6x

v = 7x → v' = 7⋅1⋅x^{1 – 1} = 7x⁰ = 7⋅1 = 7

Jadi jika f(x) = u + v, maka f ′(x) = u' + v' = 6x + 7

Contoh Soal 2

Carilah f ′(x) jika f(x) = –x³ – 8x²

Penyelesaian:

f(x) = –x³ – 8x²

Misal:

u = –x³ → u' = –3x³ ^{– 1} = –3x²

v = 8x² → v' = 8 ⋅ 2⋅ x^{2 – 1} = 16 x¹ = 16x

Jadi jika f(x) = u – v, maka f ′(x) = u' – v' = –3x² – 16x

Turunan fungsi yang berbentuk y = u⋅ v

Jika y = f(x) = u(x) ⋅ v(x), di mana turunan dari u(x) adalah u'(x) dan turunan dari v(x) adalah v'(x), maka turunan dari f(x) adalah f ′(x) = u'(x)⋅ v(x) + u(x) ⋅ v'(x). Jadi jika y = u⋅ v, maka y' = u' v + u v'.

Agar lebih jelas silahkan anda pelajarilah beberapa contoh soal berikut ini.

Contoh soal 1

Carilah y′ jika y = x(5x + 3)

Penyelesaian:

Cara 1:

y = x (5x + 3)

y = 5x² + 3x

y' = 5 ⋅ 2x^{2 – 1} + 3 ⋅1 x^{1 – 1}

y' = 10x¹ + 3 ⋅ x⁰

y' = 10x + 3 ⋅ 1

y' = 10x + 3

Cara 2:

y = x(5x + 3)

misal:

u = x → u' = 1

v = 5x + 3 → v' = 5 + 0 = 5

Jadi jika y = u⋅ v, maka

y' = u' v + u v'

y' = 1 (5x + 3) + x (5)

y' = 5x + 3 + 5x

y' = 10x + 3

Contoh soal 2

Carilah y ′ jika y = 3(2x + 1) x²

Penyelesaian:

Cara 1:

y = 3(2x + 1) x²

y = 6x³ + 3x²

y' = 6 ⋅ 3x^{3 – 1} + 3 ⋅2 x^{2 – 1}

y' = 18x² + 6x

Cara 2:

y = 3(2x + 1) x²

y = (2x + 1) 3x²

misal:

u = 2x + 1 → u' = 2

v = 3x² → v' = 6x

Jadi jika y = u⋅ v, maka

y' = u' v + u v'

y' = 2 ⋅ 3x² + (2x + 1) 6x

y' = 6x² + 12x² + 6x

y' = 18x² + 6x

Turunan fungsi yang berbentuk y = u/v

Misalnya: Carilah y ′ jika y = (x²+3x)/(5x + 3). Apakah caranya sama seperti perkalian turunan fungsi? Jika y = f(x) = u(x)/v(x), di mana turunan dari u(x) adalah u'(x) dan turunan dari v(x) adalah v'(x), maka turunan dari f(x) adalah f ′(x) = (u'(x)⋅ v(x) - u(x) ⋅ v'(x))/ v(x)². Jadi jika y = u/v, maka y' = (u'v + uv')/v².

Agar lebih jelas silahkan anda pelajarilah beberapa contoh soal berikut ini.

Contoh Soal Pembagian Turunan Fungsi

Carilah turunan pertama dari y = (3x+1)/(4x-3)

Penyelesaian:

y = (3x+1)/(4x-3)

misal:

u = 3x – 2 → u' = 3

v = 5x + 6 → v' = 5

Jika y = uv, maka

y' = (u′ v - uv′)/v²

y' = (3(5x+ 6) - (3x - 2)5)/(5x+6)²

y' = ((15x+ 18) - (15x - 10))/(5x+6)²

y' = 28/(5x+6)²

Turunan fungsi yang berbentuk y = uⁿ

Misalnya: Carilah y ′ jika y = (x²+3x)¹². Bagaiman cara mencari turunan fungsi seperti soal tersebut? Jika y = f(x) = u(x)ⁿ, di mana turunan dari u(x) adalah u'(x), maka turunan pertama dari f(x) adalah f ′(x) = n.u′(x).u(x)^n-1⋅ Jadi jika y = uⁿ, maka y' = n.u'.u^n-1

Agar lebih jelas silahkan anda pelajarilah beberapa contoh soal berikut ini.

Contoh Soal Pembagian Turunan Fungsi Pangkat

Carilah turunan pertama dari y = (2 + 5x²)⁵

Penyelesaian:

y = (2 + 5x²)⁵

misal :

u = 2 + 5x² → u' = 10x

Jika y = uⁿ, maka

y' = n. u'.u^{n – 1}

= 5. 10x (2 + 5x²)^{5 – 1} ⋅

= 50x(2 + 5x²)⁴

F. Turunan Trigonometri

Rumus Turunan Fungsi Trigonometri

Berikut ini adalah beberapa turunan dasar trigonometri yang wajib diketahui sebelum anda memecahkan persoalan turunan trigonometri:

f(x) = sin x → f ‘(x) = cos x
f(x) = cos x → f ‘(x) = −sin x
f(x) = tan x → f ‘(x) = sec2 x
f(x) = cot x → f ‘(x) = −csc2x
f(x) = sec x → f ‘(x) = sec x . tan x
f(x) = csc x → f ‘(x) = −csc x . cot x.

Perluasan Rumus Turunan Fungsi Trigonometri I

Misalkan u merupakan fungsi yang dapat diturunkan terhadap x, dimana u’ adalah turunan u terhadap x, maka :

f(x) = sin u → f ‘(x) = cos u . u’
f(x) = cos u → f ‘(x) = −sin u . u’
f(x) = tan u → f ‘(x) = sec2u . u’
f(x) = cot u → f ‘(x) = −csc2 u . u’
f(x) = sec u → f ‘(x) = sec u tan u . u’
f(x) = csc u → f ‘(x) = −csc u cot u . u’.

Perluasan Rumus Turunan Fungsi Trigonometri II

Berikut ini adalah turunan dari fungsi-fungsi rumus sin cos tan trigonometri dalam variabel sudut ax +b, dimana a dan b adalah bilangan real dengan a≠0 :

f(x) = sin (ax + b) → f ‘(x) = a cos (ax + b)
f(x) = cos (ax + b) → f ‘(x) = -a sin (ax + b)
f(x) = tan (ax + b) → f ‘(x) = a sec2 (ax +b)
f(x) = cot (ax + b) → f ‘(x) = -a csc2 (ax+b)
f(x) = sec (ax + b) → f ‘(x) = a tan (ax + b) . sec (ax + b)
f(x) = csc (ax + b) → f ‘(x) = -a cot (ax + b) . csc (ax + b).

Nah, agar kita lebih mudah menghafal sifat trigonometri diatas, mari kita kerjakan beberapa contoh soal sin cos tan dan turunan trigonometri berikut ini.

Contoh Soal Turunan Trigonometri

1.) Turunan pertama dari f(x) = 7 cos (5 – 3x) adalah f ‘ (x) = …..

Jawab :

* ingat $f(x) = {\color{Red} a.cos\:(bx+c)}\;\;\;\;maka \;\;\;\;f'(x)= {\color{Red} -ab.sin\:(bx+c)}$

* maka:

$\begin{align*}f(x) & = & 7 cos (5 - 3x)\\f'(x) & = & -7.(-3).sin(5-3x)\\ & = & 21\;sin(5-3x) \end{align*}$

2.) Jika f ‘(x) adalah turunan dari f(x) dan jika f(x) = ( 3x – 2 ) sin (2x + 1) maka f ‘ (x) adalah …

Jawab :

* $f (x) = {\color{Red} (3x-2)}\;{\color{DarkGreen} sin( 2x + 1 )}$ kita misalkan terlebih dulu

$\begin{array}{lcl}{\color{Red} u}={\color{Red} 3x-2} & maka & u'=3 \\v={\color{DarkGreen} sin(2x+1)} & maka & v'=2\;cos(2x+1) \end{array}$

* ingat rumus turunan perkalian dua fungsi :

$\begin{array}{rcl}f'(x) & = & u'.v+v'.u\\ & = & 3.{\color{DarkGreen} sin(2x+1)}+2cos(2x+1).({\color{Red} 3x-2})\\ & = & 3\;sin(2x+1)+(6x-4)\;cos(2x+1) \end{array}$

3.) Turunan pertama fungsi f (x) = 5 sin x cos x adalah f ‘ (x) = …

Jawab :

* $f (x) = {\color{Red} 5\;sin\;x}\;{\color{DarkGreen} cos\;x}$ kita misalkan terlebih dulu

$\begin{array}{lcl}{\color{Red} u}={\color{Red} 5sin\;x} & maka & u'=5cos\;x\\v={\color{DarkGreen} cos\;x} & maka & v'=-sin\;x \end{array}$

* ingat rumus turunan

$\begin{array}{rcl}f'(x) & = & u'.v+v'.u\\ & = & 5cos\;x.{\color{DarkGreen} cos\;x}+(-sin\;x).({\color{Red} 5sin\;x})\\ & = & 5\;cos^2x-5\;sin^2x\\ & = & 5(cos^2x-sin^2x)\\ & = & 5.cos\;2x \end{array}$

Namun perlu di ingat cara yang satu ini lebih simple, kita bisa pakai, berikut caranya:

* ingat bahwa 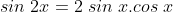$sin\;2x=2\;sin\;x.cos\;x$

* sehingga :

$\begin{align*}f(x) & = & 5\;sin\;x\;cos\;x\\ & = & \frac{5}{2}.{\color{DarkBlue} 2.sin\;x.cos\;x}\\ & = & \frac 52.sin\;2x \end{align*}$

* maka :

$\begin{align*}f'(x) & = & \frac 52.2.cos\;2x\\ & = & 5\;cos\;2x\end{align*}$

Sudah selesai deh:D sekian pembahasan tentang Turunan yang bisa saya berikan. Semoga bisa Bermanfaat bagi kalian semua yaaa. Byeeeeee:p

Yaps kali ini akan membahas materi "Limit Fungsi". Materi ini sudah mulai diperkenalkan dikelas 1 SMA right? jadi biar kalian ngga lupa yuk kita bahas lagi.

A. Limit adalah subjek matematika yang mempelajari apa yang terjadi pada suatu fungsi ketika inputnya dimasukkan mendekati suatu angka.

B. Limit Fungsi

artinya nilai x mendekati nilai a (tetapi x ≠ a) maka f(x) mendekati nilai L.

C. Sifat-Sifat Limit

Jika dan maka:
, untuk
Jika maka: untuk L ≠ 0

D. Menentukan Nilai dari Suatu

Jika f(a) = k maka
Jika maka
Jika maka
Jika atau bentuk tertentu maka sederhanakan bentuk f(x) sehingga diperoleh bentuk f(a) seperti (1), (2), dan (3).

2.3. Limit Fungsi Tak Terhingga

Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x)
Jika pangkat tertinggi f(x) lebih kecil dari pangkat tertinggi g(x)
Jika pangkat tertinggi f(x) lebih besar dari pangkat tertinggi g(x)

E. Limit Fungsi Aljabar

1. Limit Fungsi Aljabar Berhingga

Jika f(a)=C, maka nilai
Jika , maka nilai
Jika , maka nilai disederhanakan dulu menjadi bentuk 1, 2, atau 3

2. Limit Fungsi Aljabar Tak Terhingga

Menentukan nilai

atau

Jika n = m maka
Jika n > m maka
Jka n < m maka

F. Limit Fungsi Trigonometri

Untuk menghitung nilai limit fungsi trigonometri digunakan rumus-rumus berikut:

Kemudian, secara umum dapat menggunakan langkah-langkah cepat seperti di bawah ini:

Jika terdapat fungsi cos maka ubahlah ke dalam bentuk sebagai berikut:

cos x diubah menjadi
diubah menjadi

Berikut adalah sifat-sifat teorema limit fungsi trigonometri lainnya:

G. Cara Penyelesaian Limit Fungsi

Nilai limit dari suatu fungsi dapat ditentukan dengan beberapa cara, antara lain:

Substitusi Nilai dapat dicari dengan mensubstitusikan x = c ke f(x) sehingga. Penyelesaian dengan cara substitusi langsung hanya sah jika hasil akhirnya terdefinisi (tidak muncul bentuk tak tentu).
Faktorisasi
Faktorisasi dilakukan jika nilai tidak dapat dicari langsung dengan substitusi (muncul bentuk tak tentu ). Agar nilai limit tidak berupa bentuk tak tentu, maka f(x) diubah melalui faktorisasi.
Perkalian dengan akar sekawan
Perkalian dengan akar sekawan dilakukan jika dalam pengerjaan limit fungsi aljabar, ditemukan bentuk akar. Dua bentuk akar dikatakan sekawan bila kedua bentuk akar itu dikalikan akan menjadi bilangan rasional.