
Yaps kali ini akan membahas materi "Limit Fungsi". Materi ini sudah mulai diperkenalkan dikelas 1 SMA right? jadi biar kalian ngga lupa yuk kita bahas lagi.
A. Limit adalah subjek matematika yang mempelajari apa yang terjadi pada suatu fungsi ketika inputnya dimasukkan mendekati suatu angka.
B. Limit Fungsi
C. Sifat-Sifat Limit
![clip_image002[20] clip_image002[20]](https://i0.wp.com/lh6.ggpht.com/-0evucSbasIE/VIBkzxOS0cI/AAAAAAAAIYk/_JCIA2DCneI/clip_image002%25255B20%25255D%25255B4%25255D.png)
![clip_image002[36] clip_image002[36]](https://i1.wp.com/lh4.ggpht.com/-k20WY6-cWzg/VIBk2KqzVMI/AAAAAAAAIYs/0cnxHXnRzQU/clip_image002%25255B36%25255D%25255B4%25255D.png)
![clip_image002[22] clip_image002[22]](https://i1.wp.com/lh4.ggpht.com/-EqevMV4UQWA/VIBk4Yvap5I/AAAAAAAAIY0/gletBoNG70c/clip_image002%25255B22%25255D%25255B4%25255D.png)
![clip_image002[24] clip_image002[24]](https://i0.wp.com/lh5.ggpht.com/-W2rNEA29f2s/VIBk6yJ5UGI/AAAAAAAAIY8/ld4KnB-S3ls/clip_image002%25255B24%25255D%25255B4%25255D.png)
- Jika
![clip_image002[38] clip_image002[38]](https://i1.wp.com/lh4.ggpht.com/-D38_ofp9Wdc/VIBk9dl-daI/AAAAAAAAIZE/uhDSj-q-6vg/clip_image002%25255B38%25255D%25255B4%25255D.png) dan
dan ![clip_image002[40] clip_image002[40]](https://i2.wp.com/lh5.ggpht.com/-CjI-WOPKckY/VIBlA2LZavI/AAAAAAAAIZM/247Sn5a7crU/clip_image002%25255B40%25255D%25255B4%25255D.png) maka:
maka: ![clip_image002[42] clip_image002[42]](https://i0.wp.com/lh3.ggpht.com/-DFVwBZ19qrM/VIBlDX8JXQI/AAAAAAAAIZU/wi9HIloQou0/clip_image002%25255B42%25255D%25255B4%25255D.png)
![clip_image002[26] clip_image002[26]](https://i2.wp.com/lh3.ggpht.com/-k_mzqJqqd-4/VIBlEXL9PBI/AAAAAAAAIZc/k5EvdwIYkxk/clip_image002%25255B26%25255D%25255B4%25255D.png)
![clip_image002[28] clip_image002[28]](https://i0.wp.com/lh6.ggpht.com/-2sP1yaNbJiU/VIBlFh8vdAI/AAAAAAAAIZk/vE5GC8qerC0/clip_image002%25255B28%25255D%25255B4%25255D.png)
![clip_image002[30] clip_image002[30]](https://i0.wp.com/lh4.ggpht.com/-UHu9Yw6u9E8/VIBlHGZzLjI/AAAAAAAAIZs/fFAl7pT8j9I/clip_image002%25255B30%25255D%25255B4%25255D.png) , untuk
, untuk ![clip_image002[32] clip_image002[32]](https://i0.wp.com/lh5.ggpht.com/-BWw2Rzh8ALQ/VIBlI_G9aBI/AAAAAAAAIZ0/c4ZrCorEUPs/clip_image002%25255B32%25255D%25255B4%25255D.png)
- Jika
![clip_image002[44] clip_image002[44]](https://i1.wp.com/lh3.ggpht.com/-77WMMC8nBuk/VIBlKwSHB2I/AAAAAAAAIZ8/_mwlA5exSKM/clip_image002%25255B44%25255D%25255B4%25255D.png) maka:
maka: ![clip_image002[46] clip_image002[46]](https://i0.wp.com/lh3.ggpht.com/-CiHzAlVBQyM/VIBlM8tPnNI/AAAAAAAAIaE/HrqVpuL_GtY/clip_image002%25255B46%25255D%25255B4%25255D.png) untuk L ≠ 0
untuk L ≠ 0 ![clip_image002[34] clip_image002[34]](https://i1.wp.com/lh4.ggpht.com/-dC4sDJKoYGw/VIBlPRRSp-I/AAAAAAAAIaM/d052fsoUO0I/clip_image002%25255B34%25255D%25255B4%25255D.png)
D. Menentukan Nilai dari Suatu ![clip_image002[48] clip_image002[48]](https://i0.wp.com/lh3.ggpht.com/-ni6gfMYVabU/VIBlSDuuljI/AAAAAAAAIaU/2_KqP-NCn2c/clip_image002%25255B48%25255D%25255B4%25255D.png)
- Jika f(a) = k maka
![clip_image002[50] clip_image002[50]](https://i1.wp.com/lh6.ggpht.com/-2W270Nvp_b4/VIBlVOa9X4I/AAAAAAAAIac/ExTysHBoQFk/clip_image002%25255B50%25255D%25255B4%25255D.png)
- Jika
![clip_image002[52] clip_image002[52]](https://i1.wp.com/lh3.ggpht.com/-NxQhFy4k-aA/VIBlW7c37CI/AAAAAAAAIak/uUx-WN9-UEw/clip_image002%25255B52%25255D%25255B4%25255D.png) maka
maka ![clip_image002[54] clip_image002[54]](https://i2.wp.com/lh6.ggpht.com/-2S3ebUHypR4/VIBlYvpbVLI/AAAAAAAAIas/LBEwOQIVfT8/clip_image002%25255B54%25255D%25255B4%25255D.png)
- Jika
![clip_image002[56] clip_image002[56]](https://i0.wp.com/lh4.ggpht.com/-axJg7k5rdK4/VIBlZ6f0-hI/AAAAAAAAIa0/x1P6VuukTQs/clip_image002%25255B56%25255D%25255B4%25255D.png) maka
maka ![clip_image002[58] clip_image002[58]](https://i2.wp.com/lh5.ggpht.com/-SfwmthHTHWo/VIBld48dv2I/AAAAAAAAIa8/PF4kJNkBFBM/clip_image002%25255B58%25255D%25255B4%25255D.png)
- Jika
![clip_image002[60] clip_image002[60]](https://i1.wp.com/lh3.ggpht.com/-ikQ7Dsx5C6w/VIBlfmxclxI/AAAAAAAAIbE/vxZP4lDYn2w/clip_image002%25255B60%25255D%25255B4%25255D.png) atau bentuk tertentu
atau bentuk tertentu ![clip_image002[62] clip_image002[62]](https://i1.wp.com/lh5.ggpht.com/-7QDHJyMXg0Q/VIBlqQHrL7I/AAAAAAAAIbM/zyvGtIuV5G4/clip_image002%25255B62%25255D%25255B4%25255D.png) maka sederhanakan bentuk f(x) sehingga diperoleh bentuk f(a) seperti (1), (2), dan (3).
maka sederhanakan bentuk f(x) sehingga diperoleh bentuk f(a) seperti (1), (2), dan (3).
![clip_image002[64] clip_image002[64]](https://i1.wp.com/lh4.ggpht.com/-6Kj7aSyGS9U/VIBl1kIpHUI/AAAAAAAAIbU/Xs_775OS5VA/clip_image002%25255B64%25255D%25255B4%25255D.png)
![clip_image002[66] clip_image002[66]](https://i0.wp.com/lh5.ggpht.com/-25BhI_j659Y/VIBl8gRCFmI/AAAAAAAAIbc/sNUceTwxuMk/clip_image002%25255B66%25255D%25255B4%25255D.png) Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x)
Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x)![clip_image002[68] clip_image002[68]](https://i2.wp.com/lh3.ggpht.com/-vSr24t74RE4/VIBmBwD33ZI/AAAAAAAAIbk/sMNeeJTczIY/clip_image002%25255B68%25255D%25255B4%25255D.png) Jika pangkat tertinggi f(x) lebih kecil dari pangkat tertinggi g(x)
Jika pangkat tertinggi f(x) lebih kecil dari pangkat tertinggi g(x)![clip_image002[70] clip_image002[70]](https://i0.wp.com/lh4.ggpht.com/-wzlfoNkPMdY/VIBmFFZrb6I/AAAAAAAAIbs/k0yKWCZAVqw/clip_image002%25255B70%25255D%25255B4%25255D.png) Jika pangkat tertinggi f(x) lebih besar dari pangkat tertinggi g(x)
Jika pangkat tertinggi f(x) lebih besar dari pangkat tertinggi g(x)
1. Limit Fungsi Aljabar Berhingga
- Jika f(a)=C, maka nilai
![clip_image002[72] clip_image002[72]](https://i0.wp.com/lh3.ggpht.com/-KrbMjSd7Z1A/VIBmGjJMNwI/AAAAAAAAIb0/qa17RIQeSTA/clip_image002%25255B72%25255D%25255B4%25255D.png)
- Jika
![clip_image002[74] clip_image002[74]](https://i1.wp.com/lh5.ggpht.com/-bWWz4mtkwLs/VIBmIJRENVI/AAAAAAAAIb8/r4bYtVZbNcE/clip_image002%25255B74%25255D%25255B4%25255D.png) , maka nilai
, maka nilai ![clip_image002[76] clip_image002[76]](https://i1.wp.com/lh6.ggpht.com/-rFZ5qLbibc8/VIBmVtRnJQI/AAAAAAAAIcE/XVBU1mjwICU/clip_image002%25255B76%25255D%25255B4%25255D.png)
- Jika
![clip_image002[78] clip_image002[78]](https://i1.wp.com/lh6.ggpht.com/-t6vGlyLbJKs/VIBmfM85sRI/AAAAAAAAIcM/ikz0SepU1Ms/clip_image002%25255B78%25255D%25255B4%25255D.png) , maka nilai
, maka nilai ![clip_image002[82] clip_image002[82]](https://i0.wp.com/lh5.ggpht.com/-msKP2GwgLUA/VIBmogXOS2I/AAAAAAAAIcU/XfqH_33RrIg/clip_image002%25255B82%25255D%25255B4%25255D.png) disederhanakan dulu menjadi bentuk 1, 2, atau 3
disederhanakan dulu menjadi bentuk 1, 2, atau 3
2. Limit Fungsi Aljabar Tak Terhingga
Menentukan nilai- Jika n = m maka
![clip_image002[94] clip_image002[94]](https://i2.wp.com/lh3.ggpht.com/-RRRl0qbH2lE/VIBnc83PGpI/AAAAAAAAIcs/IBIvYHCf_Cg/clip_image002%25255B94%25255D%25255B4%25255D.png)
- Jika n > m maka
![clip_image002[96] clip_image002[96]](https://i1.wp.com/lh5.ggpht.com/-mzlkouAsX00/VIBnd729vUI/AAAAAAAAIc0/iyIGaziMWd0/clip_image002%25255B96%25255D%25255B4%25255D.png)
- Jka n < m maka
![clip_image002[98] clip_image002[98]](https://i0.wp.com/lh3.ggpht.com/-ktKZKTmGG3M/VIBnfXjBFDI/AAAAAAAAIc8/hyQEu7lUT2g/clip_image002%25255B98%25255D%25255B4%25255D.png)
Untuk menghitung nilai limit fungsi trigonometri digunakan rumus-rumus berikut:
- cos x diubah menjadi
![clip_image002[124] clip_image002[124]](https://i2.wp.com/lh5.ggpht.com/-1Mw5aA3TMug/VIBn92WBMPI/AAAAAAAAIek/rf2F3K4yNVk/clip_image002%25255B124%25255D%25255B4%25255D.png)
![clip_image002[126] clip_image002[126]](https://i2.wp.com/lh6.ggpht.com/-9PyquFn4Ois/VIBoHl2DeUI/AAAAAAAAIes/lDF9KmKFQ-E/clip_image002%25255B126%25255D%25255B4%25255D.png) diubah menjadi
diubah menjadi ![clip_image002[128] clip_image002[128]](https://i2.wp.com/lh6.ggpht.com/-UH97Y2Bsisc/VIBoR6eC-oI/AAAAAAAAIe0/Qhsnf4fMa5k/clip_image002%25255B128%25255D%25255B4%25255D.png)
G. Cara Penyelesaian Limit Fungsi
Nilai limit dari suatu fungsi dapat ditentukan dengan beberapa cara, antara lain:
- Substitusi Nilai
 dapat dicari dengan mensubstitusikan x = c ke f(x) sehingga
dapat dicari dengan mensubstitusikan x = c ke f(x) sehingga . Penyelesaian dengan cara substitusi langsung hanya sah jika hasil akhirnya terdefinisi (tidak muncul bentuk tak tentu
. Penyelesaian dengan cara substitusi langsung hanya sah jika hasil akhirnya terdefinisi (tidak muncul bentuk tak tentu ).
). - Faktorisasi
Faktorisasi dilakukan jika nilai tidak dapat dicari langsung dengan substitusi (muncul bentuk tak tentu ). Agar nilai limit tidak berupa bentuk tak tentu, maka f(x) diubah melalui faktorisasi.
). Agar nilai limit tidak berupa bentuk tak tentu, maka f(x) diubah melalui faktorisasi. - Perkalian dengan akar sekawan
Perkalian dengan akar sekawan dilakukan jika dalam pengerjaan limit fungsi aljabar, ditemukan bentuk akar. Dua bentuk akar dikatakan sekawan bila kedua bentuk akar itu dikalikan akan menjadi bilangan rasional.
F. Contoh soal
1. Penyelesaian dengan Metode Subtitusi langsung
2. Penyelesaian dengan Metode Memfaktorkan
Hitunglah nilai limit fungsi aljabar berikut ini:
diperoleh bentuk tak tentu maka dilakukan dengan cara memfaktorkan,
3. Penyelesaian dengan Metode Perkalian Sekawan
Hitunglah nilai limit fungsi dibawah ini:
Sampai sini saja pembahasan yang dapat saya berikan. Semoga bisa bermanfaat bagi kalian semua yaaaaaaa. Terima Kasih sudah mampir ke blog saya^^




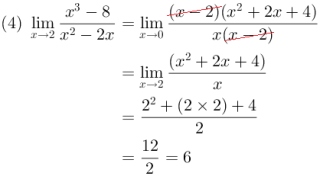






Tidak ada komentar:
Posting Komentar